实验题目描述
1.基本要求
① 很多涉及图上操作的算法都是以图的遍历操作为基础的。试写一个程序,演示在连通的无向图上访问全部结点的操作。
② 以邻接多重表为存储结构,实现连通元向图的深度优先和广度优先遍历。以用户指定的结点为起点,分别输出每种遍历下的结点访问序列和相应生成树的边集。
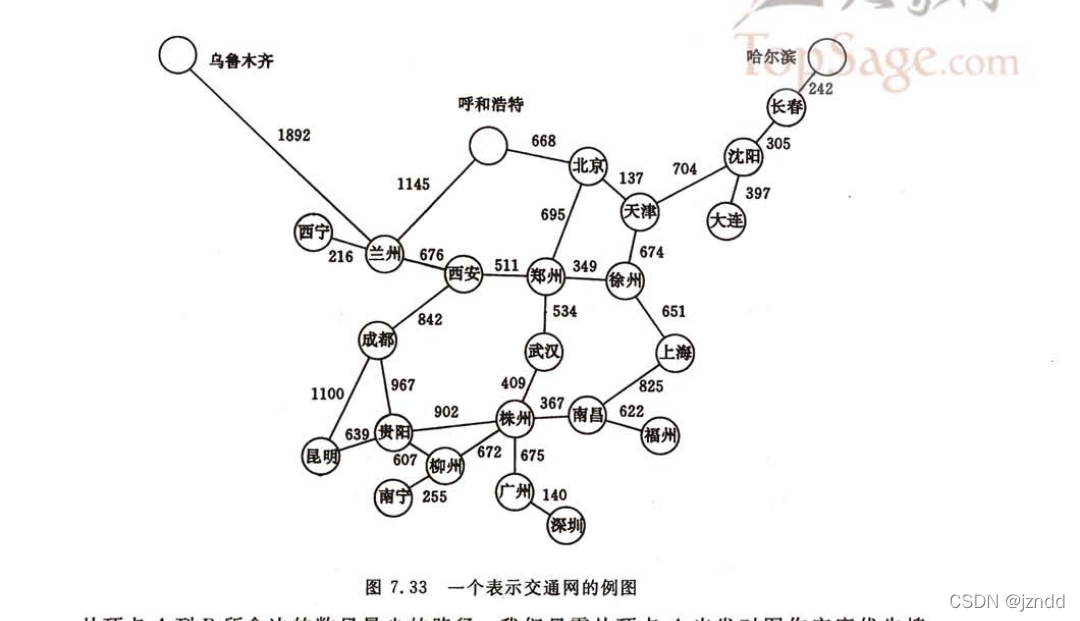
③ 自测数据:教科书图7.33 暂时忽略里程,起点为北京。
④ 设图的结点不超过30个,每个结点用一个编号表示(如果一个图有n个结点,则它们的编号分别为1,2,···,n)。通过输入图的全部边输入一个图,每个边为一个数对,可以对边的输入顺序作出某种限制。注意,生成树的边是有向边,端点顺序不能颠倒。
2.参考
利用教科书《数据结构》(紫书)图7.33的数据。
实验报告
1.题目分析及解题思路
- 问题抽象:
图的遍历是图中非常基础的应用,学习图的遍历可以参考树的先根遍历和按层次遍历,深度优先搜索过程是树的先根遍历的推广,广度优先搜索过程是树的按层次遍历的推广。
-
问题解决思路:
-
应用深度优先DFS的算法: 假设初始状态是图中所有顶点未曾被问,则深度优先搜索可从图中某个顶点v出发,访问此顶点,然后依次从v的未被访问的邻接点出发深度优先遍历图,直至图中所有和v有路径相通的顶点都被访问到;若此时图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。
按照本人的理解,深度遍历适合使用栈实现,过程大致是根节点v入栈,输出v并获得v的其中一个邻接点w1,该邻接点W1入栈,重复上述过程,直到Wi无邻接点,Wi出栈,并寻找Wi-1的邻接点,若邻接点存在,重复上述过程,若邻接点不存在,则继续出栈,直到找到某个点有邻接点为止,重复上述过程。用这种方式可以输出无向连通图的所有结点。
通过对BFS的分析过程,我们可以知道深度优先算法有极强的递归特性,因此考虑使用递归完成深度优先算法。
-
应用广度优先BFS的算法: 假设从图中某顶点v出发,在访问了v之后依次访问v的各个未曾访问过的邻接点,就后分别从这些邻接点出发依次访问它们的邻接点,并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问,直至图中所有已被访问的顶点的邻接点都被访问。若此时图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作起始点,重复上选过程,直至图中所有顶点都被访问到为止。
按照本人的理解,广度遍历适合使用队列实现,过程大致是根节点v入队并输出,然后v出队,得到v所有的邻接点W1, W2 .....Wn,W1, W2.....Wn入队并输出,然后W1出队并得到W1所有邻接点,重复上述过程,直到所有结点全部输出。总而言之,就是入队输出,出队则得邻接点,用这种方式可以输出无向连通图的所有结点。
2.实验过程(编码过程)
3.完整示例
本人关于本实验的博客https://blog.csdn.net/JackyJiang1/article/details/122747440?spm=1001.2014.3001.5501